中国女数学家首个菲尔兹奖要来了？？

就在最近，数学大佬陶哲轩激动宣布：

困扰数学家上百年的经典难题 —— 挂谷猜想（Kakeya 猜想），被北大校友王虹及哥大数学副教授 Joshua Zahl 在三维空间中证明了。

根据陶哲轩的科普，三维 Kakeya 猜想断言：

一个包含每个方向上单位长度线段的集合（Kakeya 集），在三维空间中必须具有 Minkowski 和 Hausdorff 维度等于三。（具体下文再详细展开）

虽然看起来只有一句话，但这个问题却与调和分析、数论等多个数学分支有着紧密联系，因此一直以来吸引了无数数学家竞相攻克。

现在，北大校友王虹和 Joshua Zahl 用 127 页论文证明了这一说法。

这事儿马上在国内引发诸多热议。

有人表示，一旦上述 arXiv 预印本通过审稿，凭借这一突破，王虹成为了 2026 年菲尔兹奖的热门人选。

要知道，菲尔兹奖是国际数学界最负盛名的奖项之一，被称为数学界的“诺贝尔奖”。

它旨在表彰那些在数学领域做出杰出贡献的年轻数学家（40 岁以下）。该奖项每四年颁发一次，通常在国际数学大会（International Congress of Mathematicians, ICM）上宣布获奖者。

根据平乐县宣传部的一则报道，王虹出生于 1991 年，如今只有 34 岁。如果她能够获奖，将实现“首位中国籍女性数学家获菲尔兹奖的成就”。

Kakeya 猜想：数学领域的经典难题

首先，Kakeya 猜想由日本数学家挂谷宗一（Sōichi Kakeya）于 1917 年提出，也被称为挂谷猜想。

这个问题的原型是：

一位武士在上厕所时遭到敌人袭击，矢石如雨，而他只有一根短棒，为了挡住射击，需要将短棒旋转一周 360°（支点可以变化）。但厕所很小，应当使短棒扫过的面积尽可能小。面积可以小到多少？

转换成数学表达即为：

当一根无限细的针向所有可能的方向旋转时，可以扫过的最小面积是多少？

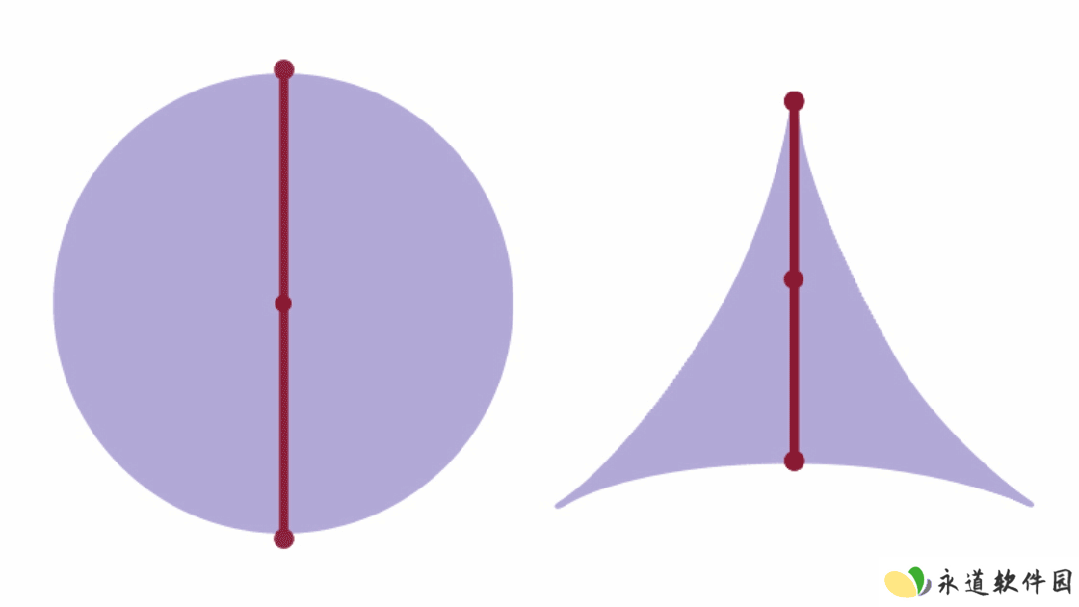
数学家将这些排列称为 Kakeya 集，在三维空间中，Kakeya 集包含了从所有方向都能看到的一根短线（单位长度的线段），而三维 Kakeya 猜想断言：

即使 Kakeya 集（R3）可能看起来非常稀疏，因为它们是由一系列的线段轨迹组成的，但其 Minkowski 维度和 Hausdorff 维度都等于 3。

其中 Minkowski 维度也被称为“盒子维度”，通过不断缩小覆盖 Kakeya 集的结构（如使用盒子或球体），可以计算出在不同尺度下覆盖集合所需的数量与尺度大小的关系。

而 Hausdorff 维度则更精细，它考虑了更细致的覆盖方式，允许使用不同大小和形状的集合来覆盖 Kakeya 集，并通过这些覆盖的最小化程度来定义维度。

当这两个维度均为 3，从数学的角度来看，这些集合在几何上与整个三维空间相同，它们在某种意义上填满了空间的大部分。

换句话说，尽管这些集合的外观可能非常稀疏，但它们实际上在几何上具有与整个空间相同的“体积”或“大小”。

以上说法转换成数学表达式如下：

使用小尺度参数（0<